ELIPSE

ELIPSE

La elipse se define como una línea curva cerrada tal que la suma de las distancias a dos puntos fijos, F y F' , llamados focos, es constante.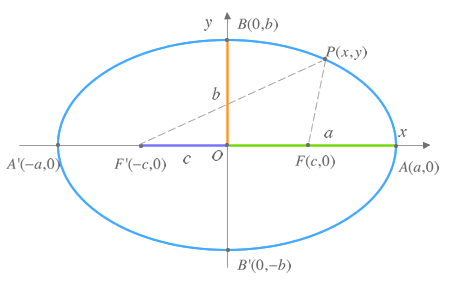

Elipse

Se trata de una circunferencia achatada que se caracteriza porque la suma de las distancias desde cualquiera de sus puntos P hasta otros dos puntos denominados focos (F y F') es siempre la misma.

Ten en cuenta que para cualquier punto de la elipse siempre se cumple que:

d(P,F)+d(P,F')=2⋅a

Donde d(P,F) y d(P,F') es la distancia de un punto genérico P al foco F y al foco F' respectivamente.

Elementos de la elipse

Los siguientes elementos se encuentran en cada elipse:

1. Centro: Es el punto de intersección de los ejes. Es, además, centro de simetría.
2. Eje principal o focal: Es el eje en el que se encuentran los focos. Es un eje de simetría.
3. Eje secundario: Es el eje perpendicular al eje principal, mediatríz del segmento que une los focos.
4. Vértices: Puntos de intersección de la elipse con los ejes.
5. Distancia focal: Distancia entre los focos. Su longitud es 2·c.
6. Semidistancia focal: Distancia entre el centro y cada foco. Su longitud es c.
7. Semieje mayor o principal: Segmento entre el centro y los vértices del eje principal. Su longitud es a.
8. Semieje menor o secundario: Segmento entre el centro y los vértices del eje secundario. Su longitud es b y cumple b=a2−c2−−−−−−√ 
9. Radio vectores: Cada punto de la elipse cuenta con dos radio vectores que son los segmentos que unen dicho punto a cada uno de los focos. Para un punto P(x , y) se cumple que d(P , F) = a -e·x y d(P, F') = a+e·x

Parábola

Parábola

Una parábola tiene vértice en el punto (–4, 2), y su directriz es y = 5, encuentre su ecuación y exprésela en la forma general.
Desarrollo
Analizando las coordenadas del vértice y la posición de la directriz, se puede concluir que:
a) La directriz es paralela al eje de las abscisas, por lo tanto la posición de la parábola es vertical.
b) La directriz corta al eje de las ordenadas en un valor (5) mayor que la ordenada del vértice (2), por lo tanto la parábola se  abre hacia abajo (sentido negativo del eje de las Y).
c) Las coordenadas del vértice no corresponden con las del origen.
d) Dado lo anterior, se trata entonces de una parábola cuya ecuación ordinaria o canónica es del tipo:

(x – h)2 = –4p (y – k)

De las coordenadas del vértice se obtiene:

h = –4

k = 2

Se obtiene p por diferencia entre las ordenadas del vértice y de la directriz, resultando:

p = 5 – 2

p = 3

Sustituyendo valores en la ecuación ordinaria, resulta:

(x – h)² = –4p(y – k)

(x – (–4))² = –4 (3) (y – (+2))

(x + 4)² = –12(y – 2)

(x + 4)² = –12y + 24

Desarrollando el binomio al cuadrado

(x + 4) (x + 4) = x² + 8x + 16

x² + 8x + 16 = +12y – 24

Simplificando e igualando a cero la ecuación se tiene:

x² + 8x + 16 + 12y – 24 = 0

x² + 8x + 12y – 8 = 0

PARABOLA

PARABOLA

LA PARÁBOLA COMO LUGAR GEOMÉTRICO

En esta oportunidad daremos algunos conceptos básicos de la parábola pero nos centraremos en su construcción como lugar geométrico. Para ello elegimos un software de descarga gratuita: Regla y compás. Incluye al final un video explicativo. Si tienen dificultad para ver las imágenes, con un click sobre ellas permite ampliarlas.

PARÁBOLA. DEFINICIÓN

La parábola es el lugar geométrico de todos los puntos del plano que equidistan de un punto fijo llamado foco y de una recta fija llamada  directriz.

Algunos elementos de la parábola: 

• Foco: es el punto fijo F
• Directriz: es la recta fija d
• Parámetro: distancia del foco a la recta directriz
• Eje: recta perpendicular a la directriz que pasa por el foco
• Vértice: punto de intersección de la parábola con su eje.
• Cuerda focal: segmento que une dos puntos de la parábola y pasa por su foco.
• Recta tangente al vértice.

CIRCUNFERENCIA

CIRCUNFERENCIA

¿dar la ecuacion de la circunferencia que tiene centro en la recta y=x+1 y que toca los puntos (1,4) y (5,2)?

Ecuación concentrica a la circunferencia y tangente a una recta

Ecuación concentrica a la circunferencia y tangente a una recta

Dos o más circunferncias son concéntricas si sus centros coinciden.

Las circunferencias concéntricas no tienen ningún punto en común.

Ejercicios

Hallar la ecuación de la circunferencia concéntrica con la ecuación , y que pasa por el punto (-3,4).

Por ser concéntricas tienen el mismo centro.

Hallar la ecuación de la circunferencia concéntrica a la circunferencia que sea tangente a la recta 3x - 4y + 7 = 0.

 

 

Ecuacion de la circunferencia conocido dos puntos y su recta una ecuación

Circunferencia que pasa por dos puntos y centro en la recta..?

Hallar la ecuación de la circunferencia que pasa por los puntos (2;3) y (-1;1) y cuyo centro está situado en la recta: x-3y-11=0. Respuesta: x^2+y^2-7x+5y-14=0

Los puntos (2;3) y (-1;1) pertenecen a la circunferencia. Entonces, en la ecuación de la circunferencia, reemplazamos "x" e "y" por las coordenadas de cada punto.

(2 - h)² + (3 - k)² = r² . . . . . . . .➊

(-1 - h)² + (1 - k)² = r² . . . . . . . ➋

Igualamos ➊ y ➋, porque ambas equivalen a r²

(2 - h)² + (3 - k)² = (-1 - h)² + (1 - k)²

4 - 4h + h² + 9 - 6k + k² = 1 + 2h + h² + 1 - 2k + k²

13 - 4h - 6k = 2 + 2h - 2k

-4h - 6k - 2h + 2k = 2 - 13

-6h - 4k = -11 . . . . . . . . . . ➌


Por otra parte, el centro (h; k) está sobre la recta x - 3y - 11 = 0. Entonces el centro verifica esta ecuación,

h - 3k - 11 = 0 . . . . . . . . . ➍

Con ➌ y ➍ formamos un sistema de ecuaciones que nos permite hallar el centro.

-6h - 4k = -11 . . . . . . . . . . ➌
h - 3k - 11 = 0 . . . . . . . . . ➍

MÉTODO DE SUSTITUCIÓN. De ➍, despejamos h ==> h = 3k + 11
Reemplazamos "h" en ➌

-6·(3k + 11) - 4k = -11

-18k - 66 - 4k = -11

-22k = -11 + 66

k = 55/(-22)

k = -5/2

Luego, h = 3k + 11 = 3·(-5/2) + 11 = 7/2

El centro es C(7/2, -5/2)


Calculamos r², reemplazando "h" y "k" en ➊

(2 - 7/2)² + (3 - (-5/2))² = r²

9/4 + 121/4 = r²

65/2 = r²


Por lo tanto, la ecuación de la circunferencia es:

(x - 7/2)² + (y - (-5/2))² = 65/2

(x -7/2)² + (y + 5/2)² = 65/2

Desarrollamos los binomios para obtener la ecuación general.

x² - 7x + 49/4 + y² + 5y + 25/4 - 65/2 = 0

▬▬▬▬▬▬▬▬▬▬▬
x² + y² - 7x + 5y -14 = 0 ◄ RESPUESTA
▬▬▬▬▬▬▬▬▬▬▬

 

Ecuación de la circunferencia conociendo dos puntos

Ecuación de la circunferencia conociendo dos puntos

Ecuación de la circunferencia

Considérese la circunferencia centrada en O(a, b) y de radio r . La condición para que un punto X(x, y) se encuentre en la misma es:

 

d(X, O) = r, es decir:

 

 

                                           (x - a)² + (y - b)² = r²                                 

 

Desarrollando los cuadrados se tiene:

 

x² - 2ax + a² + y² - 2by + b² = r²

 

x² + y² -2ax - 2by + a² + b² - r² = 0

 

Llamando A = -2a, B = -2b y C = a² + b² - r², se tiene:

 

                                      x² + y² + Ax + By + C = 0

 

Ejercicio: cálculo de la ecuación de una circunferencia

-------------------------------------------------------------------------------------------------------------------------

 Hallar la ecuación de la circunferencia centrada en el punto (5, -2) y de radio 3.

 

Resolución:

· La distancia de X(x, y) al punto (5, -2) es

 

 

· Para que el punto esté sobre la circunferencia se ha de verificar:

 

                   

   

Ecuacion de la circunferencia

Ecuacion de la circunferencia

Obtener la Ecuación de la circunferencia con centro (C) fuera del origen de las coordenadas

Tomemos, por ejemplo, la circunferencia cuyo centro está dado por C (2, ─3), con radio r = 5 que se muestra en la figura

Para obtener la ecuación general de la circunferencia que estamos viendo podemos usar dos métodos:
Método por desarrollo y
Método con las fórmulas conocidas.

Método por desarrollo

Como conocemos el centro, C (2, ─3) y el radio (r = 5) entonces la fórmula ordinaria de la circunferencia será
(x ─ a)²  +  (y ─ b)² = r² donde a y b son las coordenadas del centro C (a, b), que en nuestro caso corresponde a C (2, ─3)
entonces, nuestra ecuación ordinaria quedará como
(x ─ 2)²  +  (y ─ ─ 3)²  = 5²
(x ─ 2)²  +  (y + 3)²  = 5²
(x ─ 2)²  +  (y + 3)²  = 25
Nota: algunos usan otras letras, como (x ─ h)²  +  (y ─ k)²
 
Sigamos.
Tenemos nuestra ecuación ordinaria
(x ─ 2)²  +  (y + 3)²  = 25

Ecuación de la Circunferencia

Ecuación de la Circunferencia

Ecuacion de la Circunferencia con centro (0,0) 

Para hallar la circunferencia con centro en el origen sera necesario conocer el radio de esta o un punto por donde pasa la circunferencia, cuando se conoce el radio sera mas sencillo puesto que La ecuacion tendra como estructura   , luego al hallar el radio unicamente conoceremos la ecuacion terminada, cuando conocemos un punto de la circunferencia deberemos usar la ecuacion de distancia y hallaremos el radio.

Ejemplos:

hallar la ecuacion de la circunferencia con centro en el origen cuyo radio es 7m

CONICAS. CIRCUNFERENCIAS

CONICAS. CIRCUNFERENCIAS

Elementos de las cónicas:
Superficie: Una superficie cónica de revolución está engendrada por la rotación de una recta alrededor de otra recta fija, llamada eje, a la que corta de modo oblicuo.
Generatriz: La generatriz es una cualquiera de las rectas oblicuas.
Vértice: El vértice es el punto central donde se cortan las generatrices.
Hojas: Las hojas son las dos partes en las que el vértice divide a la superficie cónica de revolución.
Sección: Se denomina sección cónica a la curva intersección de un cono con un plano que no pasa por su vértice. En función de la relación existente entre el ángulo de conicidad (α) y la inclinación del plano respecto del eje del cono (β), pueden obtenerse diferentes secciones cónicas.

Término general de una progresion geométrica

TERMINO GENERAL DE UNA PROGRESION GEOMÉTRICA

En todas las progresiones aritméticas se puede encontrar una expresión que permite obtener cualquier término, sabiendo el lugar que ocupa. A esta expresión se le denomina término general de la progresión aritmética.

9.- Analiza la sucesión de la escena con los siguientes pasos: paso_1 Observa que cada término es igual al anterior  más la diferencia. (Cambia el valor de n para comprobarlo) paso_2 Observa que todos los términos se pueden expresar dependiendo del  primero. (Cambia el valor de n) Observa la relación que hay entre la posición de cada término y él número que multiplica a la diferencia. (Cambia el valor de n) Busca el término general de la sucesión del ejemplo. Prueba con distintas sucesiones y busca la fórmula general para cualquier sucesión. paso_3 Muestra el término general. Término general an=  a1+(n-1)*d

SUCESIONES DE NUMEROS REALES

SUCESIONES DE NUMEROS REALES

Se llama sucesión de números reales, a una agrupación infinita de elementos del conjunto R (conjunto de los números reales),

A cada uno de estos números se le llama término (primer término, segundo, etc.). De una manera matemática una sucesión se suele definir como una aplicación de N^* en R, dada por:

es decir, para n=1 tenemos el primer término, para n=2 el segundo, ...