Ecuación de la Circunferencia

Ecuación de la Circunferencia

Ecuacion de la Circunferencia con centro (0,0) 

Para hallar la circunferencia con centro en el origen sera necesario conocer el radio de esta o un punto por donde pasa la circunferencia, cuando se conoce el radio sera mas sencillo puesto que La ecuacion tendra como estructura   , luego al hallar el radio unicamente conoceremos la ecuacion terminada, cuando conocemos un punto de la circunferencia deberemos usar la ecuacion de distancia y hallaremos el radio.

Ejemplos:

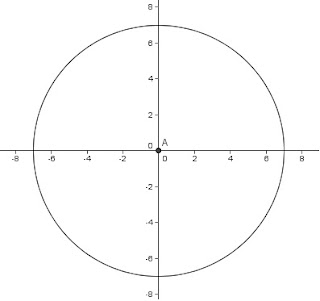
hallar la ecuacion de la circunferencia con centro en el origen cuyo radio es 7m

CONICAS. CIRCUNFERENCIAS

CONICAS. CIRCUNFERENCIAS

Elementos de las cónicas:
Superficie: Una superficie cónica de revolución está engendrada por la rotación de una recta alrededor de otra recta fija, llamada eje, a la que corta de modo oblicuo.
Generatriz: La generatriz es una cualquiera de las rectas oblicuas.
Vértice: El vértice es el punto central donde se cortan las generatrices.
Hojas: Las hojas son las dos partes en las que el vértice divide a la superficie cónica de revolución.
Sección: Se denomina sección cónica a la curva intersección de un cono con un plano que no pasa por su vértice. En función de la relación existente entre el ángulo de conicidad (α) y la inclinación del plano respecto del eje del cono (β), pueden obtenerse diferentes secciones cónicas.

Término general de una progresion geométrica

TERMINO GENERAL DE UNA PROGRESION GEOMÉTRICA

En todas las progresiones aritméticas se puede encontrar una expresión que permite obtener cualquier término, sabiendo el lugar que ocupa. A esta expresión se le denomina término general de la progresión aritmética.

9.- Analiza la sucesión de la escena con los siguientes pasos: paso_1 Observa que cada término es igual al anterior  más la diferencia. (Cambia el valor de n para comprobarlo) paso_2 Observa que todos los términos se pueden expresar dependiendo del  primero. (Cambia el valor de n) Observa la relación que hay entre la posición de cada término y él número que multiplica a la diferencia. (Cambia el valor de n) Busca el término general de la sucesión del ejemplo. Prueba con distintas sucesiones y busca la fórmula general para cualquier sucesión. paso_3 Muestra el término general. Término general an=  a1+(n-1)*d

SUCESIONES DE NUMEROS REALES

SUCESIONES DE NUMEROS REALES

Se llama sucesión de números reales, a una agrupación infinita de elementos del conjunto R (conjunto de los números reales),

A cada uno de estos números se le llama término (primer término, segundo, etc.). De una manera matemática una sucesión se suele definir como una aplicación de N^* en R, dada por:

es decir, para n=1 tenemos el primer término, para n=2 el segundo, ...

Ecuaciones Logaritmicas

Ecuaciones con Logaritmos

Son aquellas ecuaciones en las que la incógnita está acompañada del logaritmo.
Vamos a analizar la siguiente ecuación:

¿Cuánto vale x?
Has de llegar a una ecuación en la que en ambos lados del signo igual aparezcan ambos términos entre paréntesis y el símbolo del logaritmo (log) con su base por delante de cada uno de los dos miembros.
Debes comenzar a escribir la procedencia de la expresión en la cual hemos desarrollado el logaritmo.
La ecuación de donde procede es:
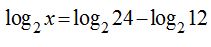
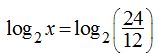
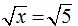Observa que tienes a ambos lados del signo = los logaritmos de dos expresiones; es como si tuvieras: (raíces en ambos lados del signo “=”). Puedes eliminar las raíces y te queda que x = 5.
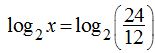Lo mismo en podemos eliminar los logaritmos: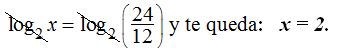

Esto es válido para cualquier valor que tenga la base.
Si tomas logaritmos en esta última expresión llegarás a (1).
Cuando en ambos lados del signo igual tengo el símbolo del logaritmo puedo eliminarlos SIEMPRE LOS TENGA A CADA TÉRMINO DENTRO DE PARÉNTESIS O CORCHETES.

ECUACIONES EXPONENCIALES

ECUACIONES EXPONENCIALES

Función exponencial

Artículo principal: Función exponencial

Las ecuaciones exponenciales también surgen cuando se quieren calcular raíces o puntos particulares de las funciones exponenciales. En la función exponencial , para saber en qué punto su gráfica corta al eje de ordenadas, se debe plantear la ecuación:

Operando se llega a la conclusión de que .
Si se quiere saber en qué punto del eje de abscisas la gráfica interseca al eje de ordenadas en el punto 1, se plantea:

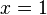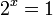
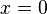
Otro ejemplo: Hallar el valor de si tal que si

ECUACIONES EXPONENCIALES

ECUACIONES EXPONENCIALES

Una ecuación exponencial es aquella ecuación en la que la incógnita aparece en el exponente.

Para resolver una ecuación exponencial vamos a tener en cuenta:

1.

2.

3. Las propiedades de las potencias.

a⁰ = 1

a¹ = a

a^m · a ⁿ = a^m+n

a^m : a ⁿ = a^{m - n}

(a^m)ⁿ = a^{m · n}

aⁿ · b ⁿ = (a · b) ⁿ

aⁿ : b ⁿ = (a : b) ⁿ

Resolución de ecuaciones exponenciales

Caso 1

Realizar las operaciones necesaria para que en los miembros tengamos la misma base, de modo que podemos igualar los exponentes.

Ejemplos

1.

2.

3.