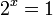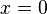matrices: diciembre 2015

lunes, 21 de diciembre de 2015

ECUACIONES EXPONENCIALES

Función exponencial

Artículo principal: Función exponencial

Las ecuaciones exponenciales también surgen cuando se quieren calcular raíces o puntos particulares de las funciones exponenciales. En la función exponencial

f\colon \mathbb {R} \to \mathbb {R} \;/\;f(x)=2^{x}\,

, para saber en qué punto su gráfica corta al eje de ordenadas, se debe plantear la ecuación:

$2^{0}=x\,$

Operando se llega a la conclusión de que

x=1\,

.
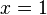Si se quiere saber en qué punto del eje de abscisas la gráfica interseca al eje de ordenadas en el punto 1, se plantea:

$2^{x}=1\,$

$x=0\,$

Otro ejemplo: Hallar el valor de

x\,

si tal que

f(x)=12

f(x)=3^{x}\,

$3^{x}=12\,$

$\log {3^{x}}=\log {12}\,$

$x={\frac {\log {12}}{\log {3}}}\approx 2{,}262$

jueves, 17 de diciembre de 2015

ECUACIONES EXPONENCIALES

Una ecuación exponencial es aquella ecuación en la que la incógnita aparece en el exponente.

Para resolver una ecuación exponencial vamos a tener en cuenta:

3. Las propiedades de las potencias.

a⁰ = 1

a¹ = a

a^m · a ⁿ = a^m+n

a^m : a ⁿ = a^{m - n}

(a^m)ⁿ = a^{m · n}

aⁿ · b ⁿ = (a · b) ⁿ

aⁿ : b ⁿ = (a : b) ⁿ

Resolución de ecuaciones exponenciales

Caso 1

Realizar las operaciones necesaria para que en los miembros tengamos la misma base, de modo que podemos igualar los exponentes.

Ejemplos

lunes, 14 de diciembre de 2015

EJERCICIOS DE PROPIEDADES DE LOGARITMOS

miércoles, 9 de diciembre de 2015

PROPIEDADES DE LOGARITMOS

1. El logaritmo de un producto es igual a la suma de los logaritmos de los factores:

Ejemplo

2. El logaritmo de un cociente es igual al logaritmo del dividendo menos el logaritmo del divisor:

Ejemplo

3. El logaritmo de una potencia es igual al producto del exponente por el logaritmo de la base:

Ejemplo

4.El logaritmo de una raíz es igual al cociente entre el logaritmo del radicando y el índice de la raíz:

Ejemplo

Resultado de imagen para propiedades de los logaritmos

jueves, 3 de diciembre de 2015

FUNCIÓN LOGARITMO

La función logarítmica en base a es la función inversa de la exponencial en base a.

Ejemplos

x
1/8	-3
1/4	-2
1/2	-1
1	0
2	1
4	2
8	3

x
1/8	3
1/4	2
1/2	1
1	0
2	−1
4	−2
8	−3

Propiedades de las funciones logarítmicas

Dominio:

Recorrido:

Es continua.

Los puntos (1, 0) y (a, 1) pertenecen a la gráfica.

Es inyectiva (ninguna imagen tiene más de un original).

Creciente si a>1.

Decreciente si a<1.

Las gráfica de la función logarítmica es simétrica (respecto a la bisectriz del 1^er y 3^er cuadrante) de la gráfica de la función exponencial, ya que son funciones reciprocas o inversas entre sí.

Definición de logaritmo

Siendo a la base, x el número e y el logaritmo.