FUNCION EXPONENCIAL NATURAL
La función exponencial de base e, 1 es conocida formalmente como la función real ex, donde e es el número de Euler, aproximadamente 2.71828...; esta función tiene por dominio de definición el conjunto de los números reales, y tiene la particularidad de que su derivada es la misma función. Se denota equivalentemente como f(x)=ex o exp(x), donde e es la base de los logaritmos naturales y corresponde a la función inversa del logaritmo natural.En términos mucho más generales, una función real E(x) se dice que es del tipo exponencial en base a si tiene la forma
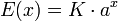

 Representación gráfica de varias funciones exponenciales.
Representación gráfica de varias funciones exponenciales.


 es la imagen de como mínimo un elemento de
es la imagen de como mínimo un elemento de  .
.
 .
.

